単一化の証明

この記事はTheorem Prover Advent Calendar 2015の7日目のために書かれました。 6日目の記事はmathinkさんのCoq で環のイデアルを作ってみるです。

タイトルの通りこの記事では（一階の）単一化についての種々の性質を証明する訳ですが、計算機科学の分野では散々研究されているテーマなのでいくらでも先行研究が存在します。 日本語で書かれた資料に限っても、少し検索すれば名古屋大学のガリグ先生が書かれたスライド[1]やお茶の水大学の方の論文[2]等々を見つけられる事でしょう。 従ってここで書かれている内容に新規性は無いに等しいのですが、別にAdvent Calendarは論文とかでは無いので恥ずかしげもなく投稿する事にします。

単一化とは？

僕の拙い解説を読むより[3]とか読んだ方が良いと思いますが… プログラミング言語の型のように、変数を含んで帰納的に定義された項があるとします。

ここで、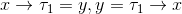といった制約を満たすためには、変数にどのような項を代入すれば良いでしょうか？ この例では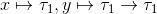を代入すれば制約が満たされる事が分かります。

このように、単一化とは与えられた制約を満たすための代入を求める事を指します。 単一化を行うためのアルゴリズムは既に良く知られており、そのアルゴリズムの健全性と完全性をCoqで証明するのが今回の最大の目的となります。

証明の方針

僕自身[1]を読んで証明をしたので殆ど同一です。強いて違いを挙げるとすれば

• 帰納的な命題で変数の集合を定義するようにした
• 行間を埋めた（[1]では証明が難しいので公理とされていた命題を全て証明した）

ぐらいでしょうか。 一応単一化を行う関数を末尾再帰に直してみたりと言った試行錯誤をしてみたのですが、可読性が著しく下がったのでここでは割愛します。

また、単一化を定義する際には定義が大変になる事を承知の上でFunctionを用いていますが、これは証明を行う際の都合でプログラムに余計な処理を追加したくなかったための措置です。 余計な引数を追加すれば確かに停止性の証明が楽になるでしょうが、実際に使うためには本来はする必要が無かった型変数の数を数える処理が必要になります。 どうやら依存型を使えば構造的な再帰で書き下す事もできるそうですが[4]、依存型を手で書き下すのもつらそうなので今回は見送りました。

対象言語

今回単一化の対象となる項の定義は以下の通りです。

Inductive t : Set :=
  | Base : t
  | Var : nat -> t
  | Fun : t -> t -> t.

名前的に大体察しが付くように、base typeが一つだけある単純型付きλ計算の型ですね。 これ以降の議論は何もこの定義に強く依存している訳ではなく、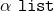や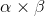等を追加するぐらいならstraightforwardにできます。

occur checkや停止性の証明で変数の集合を扱う必要がありますから、変数が項に存在する事を表す命題を定義しましょう。

Inductive In x : t -> Prop :=
  | In_Fun_dom : forall t1 t2,
      In x t1 ->
      In x (Fun t1 t2)
  | In_Fun_cod : forall t1 t2,
      In x t2 ->
      In x (Fun t1 t2)
  | In_Var : In x (Var x).

この程度の性質なら成り立つか成り立たないかを判定する関数を簡単に書き下す事ができます。

Definition In_dec : forall x t, { In x t } + { ~In x t }.
Proof.
  intros x.
  refine (fix In_dec (t0 : t) :=
    match t0 as t0' return { In x t0' } + { ~In x t0' } with
    | Base => right _
    | Var y =>
        match eq_nat_dec x y with
        | left H => left (eq_ind _ (fun y0 : nat => In x (Var y0)) (In_Var _) _ H)
        | _ => right _
        end
    | Fun t1 t2 =>
        match In_dec t1 with
        | left H => left (In_Fun_dom _ _ _ H)
        | right _ =>
            match In_dec t2 with
            | left H => left (In_Fun_cod _ _ _ H)
            | right _ => right _
            end
        end
    end); (intros H; inversion H; auto).
Defined.

停止性の証明

単一化の停止性を示すためには、変数の数と制約に含まれる項の大きさの和の辞書式順序を考えた際に、再帰呼び出しの度に引数が小さくなっている事を言わなければなりません。 この順序関係を書き下すと以下のようになります。

Definition lt constraints1 constraints2 :=
  forall n m,
  cardinal _ (fun x => In x constraints1) n ->
  cardinal _ (fun x => In x constraints2) m ->
  n <= m /\ (m <= n -> size constraints1 < size constraints2).

Coqには有限集合を扱うライブラリが標準で付いてくるのでそれを使っています。 有限集合の要素数が与えられた自然数になっているかを表す述語を使って、制約に含まれている変数の数を数える感じですね。

健全性、完全性の証明

[1]と殆ど同じように証明できました。 せっかく健全性と完全性が証明できた事ですし、証明付きの関数を書くとしたらこんな感じです。

Definition unify' : forall constraints,
  { subs | unifies subs constraints } + { ~exists subs, unifies subs constraints }.
Proof.
  intros constraints.
  remember (unify constraints) as o.
  destruct o as [ subs |].
    left.
    exists subs.
    apply unify_sound. auto.

    right.
    intros Hcontra.
    destruct Hcontra as [subs Hcontra].
    apply unify_complete in Hcontra.
    destruct Hcontra as [subs' [Hcontra]].
    congruence.
Defined.

Reference

[1] Jacques Garrigue. 一階の単一化を証明する

[2] 門脇 香子, 浅井 健一. Agda による型推論器の定式化

[3] Benjamin C. Pierce. Types and Programming Languages

[4] Conor McBride. First􏰇Order Uni􏰈cation by Structural Recursion

証明全文

今回Coqで書いた証明の全文をここに置いておきます。

Require Import Arith List Finite_sets_facts Recdef Wf_nat Omega.

Lemma Forall_map : forall X Y (P : Y -> Prop) (f : X -> Y) l,
  Forall P (map f l) <-> Forall (fun x => P (f x)) l.
Proof.
  intros X Y P f l.
  split; intros H.
    apply Forall_forall.
    intros x HListIn.
    eapply Forall_forall in H.
      apply H.
      apply in_map; auto.

    induction l as [| x l'];
      simpl;
      inversion H;
      constructor;
      auto.
Qed.

Lemma Exists_map : forall X Y (P : Y -> Prop) (f : X -> Y) l,
  Exists P (map f l) <-> Exists (fun x => P (f x)) l.
Proof.
  intros X Y P f l.
  split.
    intros HExists.
    apply Exists_exists in HExists.
    apply Exists_exists.
    destruct HExists as [x [HListIn HP]].
    apply in_map_iff in HListIn.
    destruct HListIn as [y [Heq HListIn]].
    exists y.
    subst; auto.

    intros HExists.
    apply Exists_exists in HExists.
    apply Exists_exists.
    destruct HExists as [x [HListIn HP]].
    exists (f x).
    split; auto.
    apply in_map; auto.
Qed.

Lemma Exists_preserves_Finite : forall U family,
  Forall (Finite _) family ->
  Finite _ (fun x : U => Exists (fun s => s x) family).
Proof.
  intros U family Hall.
  induction family as [| s family'].
    rewrite Extensionality_Ensembles with (B := Empty_set _).
      constructor.
      split; intros x H; inversion H.

    inversion Hall.
    rewrite Extensionality_Ensembles with (B := Union _ s (fun x : U => Exists (fun s => s x) family')).
      apply Union_preserves_Finite; auto.
      split;
        intros y HIn;
        (inversion HIn; [ left | right ]);
        auto.
Qed.

Lemma Exists_app : forall X (P : X -> Prop) l1 l2,
  Exists P (l1 ++ l2) -> Exists P l1 \/ Exists P l2.
Proof.
  intros X P l1 l2 Hexists.
  induction l1.
    auto.

    inversion Hexists.
      left. left. auto.

      assert (IHl1':  Exists P l1 \/ Exists P l2).
        apply IHl1.
        auto.
      destruct IHl1' as [IHl1' | IHl1'].
        left. right. auto.
        right. auto.
Qed.

Lemma Forall_app : forall X (P : X -> Prop) l1 l2,
  Forall P (l1 ++ l2) ->
  Forall P l1 /\ Forall P l2.
Proof.
  intros X P l1 l2 HForall.
  induction l1.
    split; auto.

    inversion HForall.
    specialize (IHl1 H2).
    destruct IHl1.
    split.
      constructor; auto.
      auto.
Qed.

Module Types.
  Inductive t : Set :=
    | Base : t
    | Var : nat -> t
    | Fun : t -> t -> t.

  Fixpoint size t :=
    match t with
    | Fun t1 t2 => S (size t1 + size t2)
    | _ => 1
    end.

  Inductive In x : t -> Prop :=
    | In_Fun_dom : forall t1 t2,
        In x t1 ->
        In x (Fun t1 t2)
    | In_Fun_cod : forall t1 t2,
        In x t2 ->
        In x (Fun t1 t2)
    | In_Var : In x (Var x).

  Definition In_dec : forall x t, { In x t } + { ~In x t }.
  Proof.
    intros x.
    refine (fix In_dec (t0 : t) :=
      match t0 as t0' return { In x t0' } + { ~In x t0' } with
      | Base => right _
      | Var y =>
          match eq_nat_dec x y with
          | left H => left (eq_ind _ (fun y0 : nat => In x (Var y0)) (In_Var _) _ H)
          | _ => right _
          end
      | Fun t1 t2 =>
          match In_dec t1 with
          | left H => left (In_Fun_dom _ _ _ H)
          | right _ =>
              match In_dec t2 with
              | left H => left (In_Fun_cod _ _ _ H)
              | right _ => right _
              end
          end
      end); (intros H; inversion H; auto).
  Defined.

  Lemma notIn_Fun : forall x t1 t2, ~In x (Fun t1 t2) -> ~In x t1 /\ ~In x t2.
  Proof.
    intros x t1 t2 HnotIn.
    split; intros HIn; apply HnotIn; [ apply In_Fun_dom | apply In_Fun_cod ]; auto.
  Qed.

  Theorem FV_Finite : forall t, Finite _ (fun x => In x t).
  Proof.
    intros t.
    induction t as [ | x | t1 IHt1 t2 IHt2 ].
      rewrite Extensionality_Ensembles with (B := Empty_set _).
        constructor.
        split; (intros x H; inversion H).
      rewrite Extensionality_Ensembles with (B := Singleton _ x).
        apply Singleton_is_finite.
        split; (intros y H; inversion H; constructor).
      rewrite Extensionality_Ensembles with
        (B := Union _ (fun x => In x t1) (fun x => In x t2)).
        apply Union_preserves_Finite; assumption.
        split; intros x H; inversion H;
          [ left | right | apply In_Fun_dom | apply In_Fun_cod ]; assumption.
  Qed.

  Fixpoint subst x t0 t :=
    match t with
    | Base => Base
    | Var y =>
        if eq_nat_dec x y then t0
        else t
    | Fun t1 t2 => Fun (subst x t0 t1) (subst x t0 t2)
    end.

  Theorem subst_In_occur : forall x t1 t2,
    In x (subst x t1 t2) -> In x t1.
  Proof.
    intros x t1 t2 HIn.
    induction t2 as [ | y | t21 IHt21 t22 IHt22 ]; simpl in * |- *.
      inversion HIn.

      destruct (eq_nat_dec x y).
        assumption.
        inversion HIn. congruence.

      inversion HIn; auto.
  Qed.

  Theorem subst_notIn : forall x t1 t2,
    ~In x t2 -> subst x t1 t2 = t2.
  Proof.
    intros x t1 t2 HnotIn.
    induction t2 as [ | y | t21 IHt21 t22 IHt22 ]; simpl in * |- *.
      reflexivity.

      destruct (eq_nat_dec x y) as [ Heq | ].
        rewrite Heq in HnotIn. exfalso. apply HnotIn. constructor.
        auto.

      destruct (notIn_Fun _ _ _ HnotIn) as [HnotIn21 HnotIn22].
      specialize (IHt21 HnotIn21).
      specialize (IHt22 HnotIn22).
      congruence.
  Qed.

  Theorem subst_In_or : forall x y t1 t2,
    In x (subst y t1 t2) -> In x t1 \/ In x t2.
  Proof.
    intros x y t1 t2 HIn.
    induction t2 as [ | x' | t21 IHt21 t22 IHt22 ]; simpl in * |- *.
      inversion HIn.

      destruct (eq_nat_dec y x') as [ Heq | ].
        rewrite <- Heq. left. auto.
        right. auto.

      inversion HIn as [t21' t22' HIn' | t21' t22' HIn' |].
        destruct (IHt21 HIn'); [ left | right; apply In_Fun_dom ]; auto.
        destruct (IHt22 HIn'); [ left | right; apply In_Fun_cod ]; auto.
  Qed.

  Definition subst_list subs t1 :=
    fold_left (fun t1 (sub : nat * t) =>
      let (x, t0) := sub in
      subst x t0 t1) subs t1.

  Lemma subst_list_app : forall subs1 subs2 t,
    subst_list (subs1 ++ subs2) t = subst_list subs2 (subst_list subs1 t).
  Proof.
    apply fold_left_app.
  Qed.

  Lemma subst_list_Base : forall subs,
    subst_list subs Base = Base.
  Proof.
    intros.
    induction subs as [| [x t] subs' IHsubs'].
      auto.
      simpl. rewrite IHsubs'. auto.
  Qed.

  Lemma subst_list_Fun : forall subs t1 t2,
    subst_list subs (Fun t1 t2) = Fun (subst_list subs t1) (subst_list subs t2).
  Proof.
    intros subs.
    induction subs as [| [x t] subs']; intros t1 t2; simpl; eauto.
  Qed.

  Notation unifies subs t1 t2 :=
    (subst_list subs t1 = subst_list subs t2).

  Lemma subst_preserves_unifies : forall x t0 subs t,
    unifies subs (Var x) t0 ->
    unifies subs t (subst x t0 t).
  Proof.
    intros x t0 subs t Hunifies.
    induction t as [ | y | t1 IHt1 t2 IHt2 ]; simpl in * |- *.
      auto.
      destruct (eq_nat_dec x y); congruence.
      repeat rewrite subst_list_Fun. f_equal; auto.
  Qed.

  Lemma unifies_occur : forall x t,
    Var x <> t -> In x t -> forall subs, ~unifies subs (Var x) t.
  Proof.
    intros x t Hneq Hoccur subs Hunifies.
    assert (size (subst_list subs (Var x)) >= size (subst_list subs t)).
      rewrite Hunifies.
      constructor.
    clear Hunifies.
    induction Hoccur as [ t1 t2 HIn IHHoccur | t1 t2 HIn IHHoccur | ].
      rewrite subst_list_Fun in H.
      simpl in H.
      apply IHHoccur; [ intros Heq; rewrite Heq in H | ]; omega.

      rewrite subst_list_Fun in H.
      simpl in H.
      apply IHHoccur; [ intros Heq; rewrite Heq in H | ]; omega.

      auto.
  Qed.
End Types.

Module Constraint.
  Definition t := (Types.t * Types.t)%type.

  Definition size constraints :=
    fold_right plus 0
      (map (fun c : t =>
        let (t1, t2) := c in
        Types.size t1 + Types.size t2) constraints).

  Definition In x constraints :=
    Exists (fun c : t =>
      let (t1, t2) := c in
      Types.In x t1 \/ Types.In x t2) constraints.

  Lemma FV_Finite : forall constraints, Finite _ (fun x => In x constraints).
  Proof.
    intros constraints.
    unfold In.
    rewrite Extensionality_Ensembles with
      (B := fun x => Exists (fun s => s x) (map (fun c : t =>
        let (t1, t2) := c in
        Union _ (fun x => Types.In x t1) (fun x => Types.In x t2)) constraints)).
    apply Exists_preserves_Finite.
    apply Forall_map.
    apply Forall_forall.
    intros [t1 t2] HIn.
    apply Union_preserves_Finite; apply Types.FV_Finite.

    split;
      intros x HIn;
      [ apply Exists_map | apply Exists_map in HIn ];
      apply Exists_exists in HIn;
      apply Exists_exists;
      destruct HIn as [[t1 t2] [HListIn HIn]];
      exists (t1, t2);
      (split;
        [ auto
        | destruct HIn; [left | right]; auto ]).
  Qed.

  Definition subst x t0 constraints :=
    map (fun c : t => 
      let (t1, t2) := c in
      (Types.subst x t0 t1, Types.subst x t0 t2)) constraints.

  Theorem subst_In_occur : forall x t constraints,
    In x (subst x t constraints) -> Types.In x t.
  Proof.
    intros x t constraints HIn.
    induction constraints as [| [t1 t2] constraints' IHconstraints']; simpl in * |- *.
      inversion HIn.

      inversion HIn as [[t1' t2'] constraints'' Hor |]; subst.
        destruct Hor as [HIn' | HIn'];
        eapply Types.subst_In_occur;
        apply HIn'.

        apply IHconstraints'.
        auto.
  Qed.

  Theorem subst_In_or : forall x y t constraints,
    In x (subst y t constraints) -> Types.In x t \/ In x constraints.
  Proof.
    intros x y t constraints HIn.
    induction constraints as [| [t1 t2] constraints' IHconstraints']; simpl in * |- *.
      inversion HIn.

      inversion HIn as [[t1' t2'] constraints'' Hor | [t1' t2'] constraints'' HIn' ]; subst.
        destruct Hor as [HIn' | HIn'];
        (destruct (Types.subst_In_or _ _ _ _ HIn');
          [left | right; left]; auto).

        destruct (IHconstraints' HIn'); [ left | right; right ]; auto.
  Qed.

  Notation subst_list subs constraints :=
    (map (fun p : t =>
      let (t1, t2) := p in
      (Types.subst_list subs t1, Types.subst_list subs t2)) constraints).

  Lemma subst_list_app : forall subs1 subs2 constraints,
    subst_list (subs1 ++ subs2) constraints = subst_list subs2 (subst_list subs1 constraints).
  Proof.
    intros subs1 subs2 constraints.
    rewrite map_map.
    apply map_ext.
    intros [t1 t2].
    f_equal; apply Types.subst_list_app.
  Qed.

  Notation unifies subs constraints :=
    (Forall (fun p : t =>
      let (t1, t2) := p in
      Types.unifies subs t1 t2) constraints).

  Theorem subst_preserves_unifies : forall x t0 subs constraints,
    Types.unifies subs (Types.Var x) t0 ->
    unifies subs constraints ->
    unifies subs (subst x t0 constraints).
  Proof.
    intros x t0 subs constraints Hunifies Hunifies'.
    unfold subst.
    apply Forall_map.
    eapply Forall_impl; [| apply Hunifies'].
    intros [t1 t2] Hunifies''.
    repeat rewrite <- (Types.subst_preserves_unifies _ _ _ _ Hunifies).
    auto.
  Qed.

  Lemma unify_sound_same : forall t subs constraints,
    unifies subs constraints ->
    unifies subs ((t, t) :: constraints).
  Proof.
    intros t subs constraints Hunifies.
    constructor; auto.
  Qed.

  Lemma unify_complete_same : forall t subs constraints,
    unifies subs ((t, t) :: constraints) ->
    unifies subs constraints.
  Proof.
    intros t subs constraints Hunifies.
    inversion Hunifies.
    auto.
  Qed.

  Lemma unify_sound_subst : forall x t l constraints,
    ~Types.In x t ->
    unifies l (subst x t constraints) ->
    unifies ((x, t) :: l) ((Types.Var x, t) :: constraints).
  Proof.
    intros x t l constraints Hoccur Hunifies.
    constructor.
      simpl.
      destruct (eq_nat_dec x x).
        rewrite Types.subst_notIn; auto.
        exfalso. auto.
      
      unfold subst in Hunifies.
      apply Forall_map in Hunifies.
      eapply Forall_impl; [| apply Hunifies ].
      intros [t0 t3] Heqsubst.
      simpl in Heqsubst.
      auto.
  Qed.

  Lemma unify_sound_comm : forall t1 t2 subs constraints,
    unifies subs ((t2, t1) :: constraints) ->
    unifies subs ((t1, t2) :: constraints).
  Proof.
    intros t1 t2 subs constraints Hunifies.
    inversion Hunifies.
    constructor; auto.
  Qed.

  Lemma unify_sound_fun : forall constraints t11 t12 t21 t22 subs,
    unifies subs ((t11, t21) :: (t12, t22) :: constraints) ->
    unifies subs ((Types.Fun t11 t12, Types.Fun t21 t22) :: constraints).
  Proof.
    intros constraints t11 t12 t21 t22 subs Hunifies.
    inversion Hunifies as [| x l Hunifies1 Hunifies'].
    inversion Hunifies'.
    constructor.
      repeat rewrite Types.subst_list_Fun. f_equal; auto.
      auto.
  Qed.

  Lemma unify_complete_fun : forall constraints t11 t12 t21 t22 subs,
    unifies subs ((Types.Fun t11 t12, Types.Fun t21 t22) :: constraints) ->
    unifies subs ((t11, t21) :: (t12, t22) :: constraints).
  Proof.
    intros constraints t11 t12 t21 t22 subs Hunifies.
    inversion Hunifies as [| [t1 t2] l Hunifies1 Hunifies'].
    repeat rewrite Types.subst_list_Fun in Hunifies1.
    inversion Hunifies1.
    repeat (constructor; auto).
  Qed.

  Definition lt constraints1 constraints2 :=
    forall n m,
    cardinal _ (fun x => In x constraints1) n ->
    cardinal _ (fun x => In x constraints2) m ->
    n <= m /\ (m <= n -> size constraints1 < size constraints2).

  Lemma lt_well_founded : well_founded lt.
  Proof.
    intros constraints1.
    destruct (finite_cardinal _ _ (FV_Finite constraints1)) as [n Hcardinal1].
    generalize dependent constraints1.
    induction n as [n IHn] using lt_wf_ind.
    intros constraints1 Hcardinal1.
    induction constraints1 as [constraints1 IHconstraints1] using (induction_ltof1 _ size).
    constructor.
    intros constraints2 Hlt.
    destruct (finite_cardinal _ _ (FV_Finite constraints2)) as [m Hcardinal2].
    destruct (Hlt _ _ Hcardinal2 Hcardinal1) as [Hcard Hsize].
    destruct (eq_nat_dec m n) as [Heq |].
      rewrite Heq in * |- *.
      apply IHconstraints1; [ apply Hsize |]; auto.

      apply IHn with (m := m).
        omega.
        auto.
  Qed.

  Lemma lt_subst : forall constraints x t t1 t2,
    ~Types.In x t ->
    (t1 = t /\ t2 = Types.Var x \/ t1 = Types.Var x /\ t2 = t) ->
    lt (subst x t constraints) ((t1, t2) :: constraints).
  Proof.
    intros constraints x t t1 t2 HnotIn HVar m n Hcardinal1 Hcardinal2.
    assert (Hinclst: Strict_Included _ (fun y => In y (subst x t constraints)) (fun y => In y ((t1, t2) :: constraints))).
    split.
      intros y HIn.
      apply subst_In_or in HIn.
      destruct HIn as [ HIn | HIn ].
        left. destruct HVar as [[Ht1 Ht2] | [Ht1 Ht2]]; subst; auto.
        right. auto.

      intros Hcontra.
      assert (HnotIncluded: ~Included _ (fun y => In y ((t1, t2) :: constraints)) (fun y => In y (subst x t constraints))).
        intros HIncluded.
        specialize (HIncluded x).
        assert (HIn: In x ((t1, t2) :: constraints)).
          destruct HVar as [[Ht1 Ht2] | [Ht1 Ht2]]; subst; left; [right | left]; constructor.
        specialize (HIncluded HIn).
        apply subst_In_occur in HIncluded.
        auto.
      apply HnotIncluded.
      rewrite Hcontra.
      intros y H.
      auto.

    specialize (incl_st_card_lt _ _ _ Hcardinal1 _ _ Hcardinal2 Hinclst).
    intros.
    omega.
  Qed.

  Lemma lt_fun : forall t11 t12 t21 t22 constraints,
    lt ((t11, t21) :: (t12, t22) :: constraints) ((Types.Fun t11 t12, Types.Fun t21 t22) :: constraints).
  Proof.
    intros t11 t12 t21 t22 constraints m n Hcardinal1 Hcardinal2.
    split.
      apply (incl_card_le _ _ _ _ _ Hcardinal1 Hcardinal2).
      intros x HIn.
      inversion HIn as [[t11' t21'] constraints' Hor | [t11' t21'] constraints' HIn' ].
        left.
        destruct Hor; [left | right]; apply Types.In_Fun_dom; auto.

        inversion HIn' as [[t12' t22'] constraints'' Hor | ].
          left.
          destruct Hor; [left | right]; apply Types.In_Fun_cod; auto.

          right.
          auto.

      intros.
      unfold size.
      simpl.
      omega.
  Qed.

  Lemma lt_cons : forall c constraints,
    lt constraints (c :: constraints).
  Proof.
    intros [t1 t2] constraints m n Hcardinal1 Hcardinal2.
    split.
      apply (incl_card_le _ _ _ _ _ Hcardinal1 Hcardinal2).
      intros x HIn.
      right.
      auto.

      intros.
      unfold size.
      simpl.
      assert (0 < Types.size t1).
        induction t1; simpl; omega.
      omega.
  Qed.

  Function unify constraints { wf lt constraints } :=
    match constraints with
    | nil => Some nil
    | (Types.Base, Types.Base) :: constraints' =>
        unify constraints'
    | (Types.Var x, Types.Var y) :: constraints'  =>
        if eq_nat_dec x y then unify constraints'
        else option_map (cons (x, Types.Var y)) (unify (subst x (Types.Var y) constraints'))
    | (Types.Var x, t2) :: constraints' =>
        if Types.In_dec x t2 then None
        else option_map (cons (x, t2)) (unify (subst x t2 constraints'))
    | (t1, Types.Var y) :: constraints' =>
        if Types.In_dec y t1 then None
        else option_map (cons (y, t1)) (unify (subst y t1 constraints'))
    | (Types.Fun t11 t12, Types.Fun t21 t22) :: constraints' =>
        unify ((t11, t21) :: (t12, t22) :: constraints')
    | _ => None
    end.
  Proof.
    intros.
    apply lt_cons.

    intros.
    apply lt_subst; auto.

    intros.
    apply lt_subst; auto.

    intros.
    apply lt_cons.

    intros.
    apply lt_subst; auto.
    intros H.
    inversion H.
    auto.

    intros.
    apply lt_subst; auto.
    
    intros.
    apply lt_subst; auto.

    intros.
    apply lt_fun.

    apply lt_well_founded.
  Qed.

  Theorem unify_sound : forall constraints subs,
    unify constraints = Some subs -> unifies subs constraints.
  Proof.
    intros constraints.
    functional induction (unify constraints);
      intros subs Hunify;
      try solve [inversion Hunify];
      try (apply unify_sound_same; auto).

      constructor.

      destruct (unify (subst x (Types.Var y) constraints')); inversion Hunify.
      apply unify_sound_subst.
        intros H. inversion H. auto.
        auto.

      destruct (unify (subst x t2 constraints')); inversion Hunify.
      apply unify_sound_subst; auto.

      destruct (unify (subst y t1 constraints')); inversion Hunify.
      apply unify_sound_comm.
      apply unify_sound_subst; auto.

      apply unify_sound_fun.
      auto.
  Qed.

  Notation moregen subs subs' :=
    (exists subs0, forall t, Types.subst_list subs' t = Types.subst_list subs0 (Types.subst_list subs t)).

  Lemma moregen_extend : forall subs x t subs',
    Types.unifies subs (Types.Var x) t ->
    moregen subs' subs ->
    moregen ((x, t) :: subs') subs.
  Proof.
    intros subs x t0 subs' Hunifies Hmoregen.
    destruct Hmoregen as [ subs0 Hmoregen' ].
    exists subs0.
    intros t1.
    simpl.
    rewrite <- Hmoregen'.
    rewrite <- Types.subst_preserves_unifies; auto.
  Qed.

  Lemma unify_complete_subst : forall x t subs constraints,
    ~Types.In x t ->
    (forall subs,
      unifies subs (subst x t constraints) ->
      exists subs',
        unify (subst x t constraints) = Some subs' /\ moregen subs' subs) ->
    unifies subs ((Types.Var x, t) :: constraints) ->
    exists subs',
      option_map (cons (x, t)) (unify (subst x t constraints)) = Some subs' /\ moregen subs' subs.
  Proof.
    intros x t subs constraints Hoccur IH Hunifies.
    inversion Hunifies as [| [t1 t2] l' Hu Hunifies'].
    apply (subst_preserves_unifies _ _ _ _ Hu) in Hunifies'.
    specialize (IH _ Hunifies').
    destruct IH as [subs' [Heq Hmoregen]].
    rewrite Heq.
    exists ((x, t) :: subs').
    split.
      reflexivity.
      apply moregen_extend; auto.
  Qed.
      
  Theorem unify_complete : forall constraints subs,
    unifies subs constraints ->
    exists subs', unify constraints = Some subs' /\ moregen subs' subs.
  Proof.
    intros constraints.
    functional induction (unify constraints); intros subs Hunifies;
      try (apply unify_complete_same in Hunifies; auto).
      exists nil.
      split.
        auto.
        exists subs. auto.

      apply unify_complete_subst; auto.
      inversion Hunifies as [| [t1' t2'] constraints'' Hunifies'].
      intros Hcontra.
      inversion Hcontra.
      auto.

      inversion Hunifies as [| [t1' t2'] constraints'' Hunifies'].
      exfalso.
      apply Types.unifies_occur with (subs := subs) (x := x) (t := t2); auto.
      destruct t2; inversion y; intros Hcontra; inversion Hcontra.

      apply unify_complete_subst; auto.

      inversion Hunifies as [| [t1' t2'] constraints'' Hunifies'].
      exfalso.
      apply Types.unifies_occur with (subs := subs) (x := y) (t := t1); auto.
      destruct t1; inversion y0; intros Hcontra; inversion Hcontra.

      apply unify_sound_comm in Hunifies.
      apply unify_complete_subst; auto.

      apply unify_complete_fun in Hunifies.
      auto.

      destruct constraints as [| [t1 t2] ]; [ | destruct t1; destruct t2 ]; inversion y;
        inversion Hunifies as [| [t1 t2] l Hcontra];
        rewrite Types.subst_list_Fun in Hcontra;
        rewrite Types.subst_list_Base in Hcontra;
        inversion Hcontra.
  Qed.

  Definition unify' : forall constraints,
    { subs | unifies subs constraints } + { ~exists subs, unifies subs constraints }.
  Proof.
    intros constraints.
    remember (unify constraints) as o.
    destruct o as [ subs |].
      left.
      exists subs.
      apply unify_sound. auto.

      right.
      intros Hcontra.
      destruct Hcontra as [subs Hcontra].
      apply unify_complete in Hcontra.
      destruct Hcontra as [subs' [Hcontra]].
      congruence.
  Defined.
End Constraint.